题目描述
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
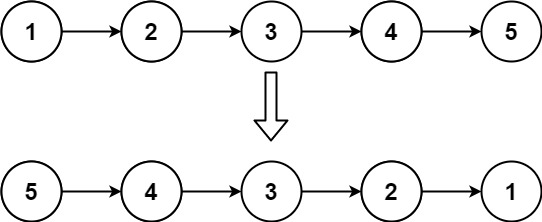
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]示例 2:
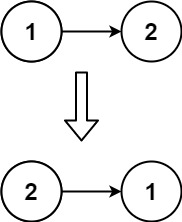
输入:head = [1,2]
输出:[2,1]示例 3:
输入:head = []
输出:[]提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
思路及解答
双指针解法(迭代解法)
如果再定义一个新的链表,实现链表元素的反转,其实这是对内存空间的浪费。
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
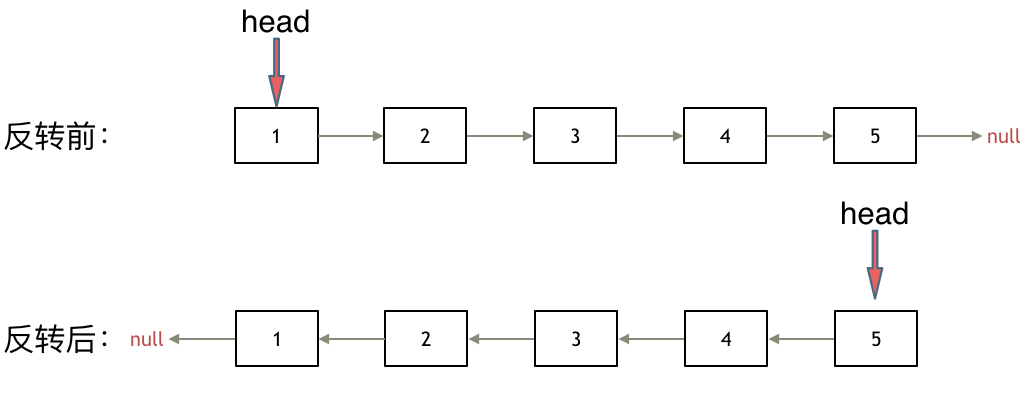
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
双指针反转:
- 首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
- 开始反转:把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。 - 接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
- 最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时return pre指针就可以了,pre指针就指向了新的头结点。
// 双指针
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// 由于单链表的结构,至少要用三个指针才能完成迭代反转
// cur 是当前遍历的节点,pre 是 cur 的前驱结点,temp 是 cur 的后继结点
ListNode prev = null;
ListNode cur = head;
ListNode temp = null;
while (cur != null) {
temp = cur.next;// 保存下一个节点
cur.next = prev;//当前节点指向prev节点
prev = cur;
cur = temp;
}
return prev;
}
}上面操作单链表的代码逻辑不复杂,而且也不止这一种正确的写法。但是操作指针的时候,有一些很基本、很简单的小技巧,可以让你写代码的思路更清晰:
需要注意循环的终止条件。要知道循环终止时,各个指针的位置,这样才能保返回正确的答案。如果你觉得有点复杂想不清楚,那就动手画一个最简单的场景跑一下算法,比如这道题就可以画一个只有两个节点的单链表 1->2,然后就能确定循环终止后各个指针的位置了。
递归解法
上面的迭代解法操作指针虽然有些繁琐,但是思路还是比较清晰的。如果现在让你用递归来反转单链表,有没啥想法?对于刚开始刷题的小伙伴来说,可能很难想到,这很正常。如果有解过二叉树系列算法题,回头再来看这道题,就有可能有想法解这道题了。因为二叉树结构本身就是单链表的延伸,相当于是二叉链表嘛,所以二叉树上的递归思维,套用到单链表上是一样的。
递归反转单链表的关键在于,这个问题本身是存在子问题结构的。
例如,现在给你输入一个以 1 为头结点单链表 1->2->3->4,那么如果忽略这个头结点 1,只拿出 2->3->4 这个子链表,它也是个单链表对吧?
那么这个 reverseList 函数,只要输入一个单链表,就能给我反转对吧?那么能不能用这个函数先来反转 2->3->4 这个子链表呢,然后再想办法把 1 接到反转后的 4->3->2 的最后面,是不是就完成了整个链表的反转?
也就是
reverseList(1->2->3->4) = reverseList(2->3->4) -> 1这就是「分解问题」的思路,通过递归函数的定义,把原问题分解成若干规模更小、结构相同的子问题,最后通过子问题的答案组装原问题的解。
class Solution {
// 定义:输入一个单链表头结点,将该链表反转,返回新的头结点
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode last = reverseList(head.next);
head.next.next = head;
head.next = null;
return last;
}
}对于「分解问题」思路的递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverseList 函数定义是这样的:输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
明白了函数的定义,再来看这个问题,这段代码似乎就很好理解了
借用栈
借用栈先进后出的能力(或者双端队列,一端进,另一端出也是一样的效果)
- 首先将所有的结点入栈
- 然后创建一个虚拟虚拟头结点,让cur指向虚拟头结点。然后开始循环出栈,每出来一个元素,就把它加入到以虚拟头结点为头结点的链表当中,最后返回即可。
class Solution {
public ListNode reverseList(ListNode head) {
// 如果链表为空,则返回空
if (head == null) return null;
// 如果链表中只有只有一个元素,则直接返回
if (head.next == null) return head;
// 声明一个双端队列
ArrayDeque<ListNode> stack = new ArrayDeque<>();
ListNode cur = head;
while (cur != null) {
stack.push(cur);
cur = cur.next;
}
// 创建一个虚拟头结点
ListNode pHead = new ListNode(0);
cur = pHead;
while (!stack.isEmpty()) {
ListNode node = stack.pop();
cur.next = node;
cur = cur.next;
}
// 最后一个元素的next要赋值为空
cur.next = null;
return pHead.next;
}
}解法总结
最好的方式还是双指针解法;如果数据量较大,递归解法和借用栈的方式都有可能导致栈溢出的情况
