位图

概述

有100亿个无符号整型数据，给定一个数据，如何判断这个数据是否在这个100亿个数据中。

有人说可以进行排序，再进行遍历或二分查找；这里先不谈算法效率的问题，这100亿数据如何在能否在内存中放下也是一个问题。

如果用int类型来存储这100亿个数据，那么就需要 100亿 * 4字节 = 37GB ≈ 40GB

所以这些方法行不通的根本原因实际上是内存不够。

位图

实际上只需要判断数据是否存在，可以我0表示存在，1表示不存在。那么在程序中，就可以使用最小的单位bit来进行表示，1个bit就有两种取值：0和1。所以位图其实就是一种直接定址法的哈希，只不过位图只能表示这个值在或者不在。

假设目前数字25存在，那么就可以直接把第25位置为1。其他为0的则表示不存在这个数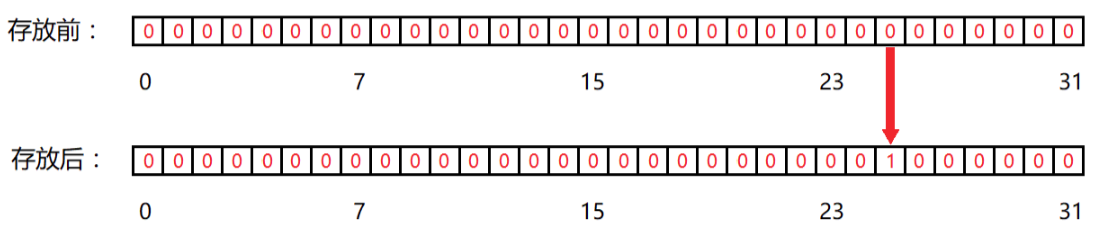

那么现在存储100亿个数据就需要 100亿 * 1bit = 1.2GB

位图的缺点

位图存储的元素大小受限于存储空间的大小。比如，1K 字节内存，能存储 8K 个值且大小上限为 8K 的元素
- 比如，要存储值为 65535 的数，就需要8Kb的内存。这就有可能导致大量的内存浪费。也就是说，在数据比较稠密的情况下，位图算法能够节约存储空间，但是如果数据稀疏且值较大，存储空间同样会存在一定程度的浪费。基于此，就提出了位图的改进版 - 稀疏位图
不能存储真实数据值，即只能判断数据存在不存在，且只适用于整数型数据。如果判断字符串以及其他类型数据存在与否，此时就可以使用布隆过滤器

稀疏位图

较为经典的位图压缩算法RoaringBitmap

RoaringBitmap的核心思想就是，将32位无符号整数按照高16位分桶，即最多可能有 2^16=65536 个桶，高16位的值作为其桶的索引，每个桶对应一个容器container。存储数据时，按照数据的高16位找到container（找不到就会新建一个），再将低16位放入container中。也就是说，Roaring将Bitmap从一层的连续存储，转换为一个二级的存储结构

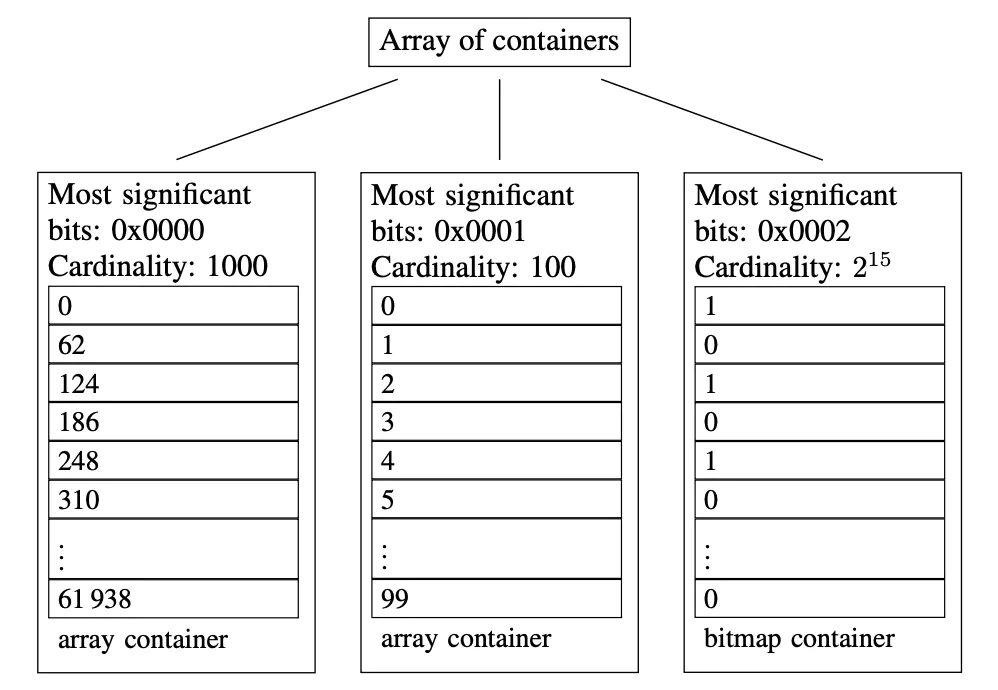
图中示例(这只是例子)：

高16位为0000H的container，存储有前1000个62的倍数。
高16位为0001H的container，存储有[2^16, 2^16+100)区间内的100个数。
高16位为0002H的container，存储有[2×2^16, 3×2^16)区间内的所有偶数，共215个。

实际上，container容器的结构有三种类型：有序数组、未压缩位图、和行程长度编码。

区间内数据较多，且分布零散，则选择（未压缩）位图。当低16位中，元素个数大于4096时，则使用（未压缩）位图
区间内数据较少，且分布零散，则选择使用有序数组。当低16位中，元素个数小于4096时，采用有序数组的结构进行存储。在查找元素时，使用二分查找方法。
区间内数据连续分布，则选择用Run Length Encoding编码。行程长度编码是一种无损数据压缩技术，其原理是，将连续出现的数据存储为起始值和计算两部分。比如，数据列表[1,2,3,4,5,6]存储为[1,5]，表示以1开始，后面连续递增5个数值。

在进行插入和删除操作之后，需要根据元素个数进行容器转换。插入元素时，若元素个数达到4096，则需要转换为未压缩位图进行存储。删除元素时，若元素个数小于4096时，则需要转换为有序数组存储。

那么这里为什么阈值选择的是4096呢？
论文中提到，由于container中只需要存储低16位的数，那么数组存储的时候是使用2字节即16 bit的short类型存储的，那么数组中存一个数字就是2字节，存4096个数字就是 8KB
而当需要存储的数字大于4096个数后，可以使用2^16 bit 的位图来存储，2^16 bit 的位图的存储空间恒等于8KB，有某一个数字，就把那个位置为1，没有就置为0
如下图所示，显然当元素个数小于4096时，占用空间就是元素个数 * 2B < 8KB;当元素个数大于4096时，占用空间就是8KB

Roaring 提供O(logn)的查找性能：

首先二分查找key值的高16位是否在分片（chunk）中
如果分片存在，则查找分片对应的Container是否存在
- 如果Bitmap Container，查找性能是O(1)
- 其它两种Container，需要进行二分查找

因此RoaringBitMap尽量节省空间，但也同时影响了效率，相当于时间换空间。