概述
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,查询时可以用来判断 “一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。
原理
当一个元素被加入集合时,通过 K 个散列函数将这个元素映射成一个位图中的 K 个位置,把它们置为 1。查询时,只要查看这些位置是不是都是 1 ,就知道集合中有没有它了:如果这些位置有任何一个 0,则被查询元素一定不存在;如果都是 1,则被查询元素很可能存在。
简单来说就是将一个长度为 m 的位数组的所有元素初始化为 0,用 k 个散列函数对元素进行 k 次散列运算跟 len (m) 取余得到 k 个位置并将 m 中对应位置设置为 1。

如上图,位数组的长度是8,散列函数个数是 3,两个元素x,y。这两个元素都经过三次哈希函数生成三个哈希值,并映射到位数组的不同的位置,并置为1。元素 x 映射到位数组的第0位,第4位,第7位,元素y映射到数组的位数组的第1位,第4位,第6位。
当布隆过滤器保存的元素越多,被置为 1 的 bit 位也会越来越多,元素 z 即便没有存储过,假设哈希函数将z映射到位数组的三个位都被其他值设置为 1 了,对于布隆过滤器的机制来讲,元素 z 这个值也是存在的,也就是说布隆过滤器存在一定的误判率。因此布隆过滤器只能保证一定不存在和可能存在。
误判率
布隆过滤器包含如下四个属性:
- k : 哈希函数个数
- m : 位数组长度
- n : 插入的元素个数
- p : 误判率
若位数组长度太小则会导致所有 bit 位很快都会被置为 1 ,那么检索任意值都会返回“可能存在” , 起不到过滤的效果。位数组长度越大,则误判率越小。同时,哈希函数的个数也需要考量,哈希函数的个数越大,检索的速度会越慢,误判率也越小,反之,则误判率越高。
为什么就用一个hash函数不行?
其实布隆过滤器底层是用 位图 实现的,而多个hash函数就是为了减少位图的误判率的。具体可往下看
假设布隆过滤器中的hash函数满足simple uniform hashing假设:每个元素都等概率地hash到m个位中的任何一个,与其它元素被hash到哪个位无关。那么
- 1 次hash函数后 某一个bit 被置为1的概率为:$1/m$
- 1次hash函数后 某一个bit 未被置为1的概率为:$1 - 1/m$
- k次hash函数某一个bit 未被置为1的概率为:$(1 - 1/m)^k$
- 如果插入了n个元素,某一个bit 都 未被置为1的概率为:$(1 - 1/m)^{nk}$
- 那么这个位被 置为 1的 概率就为:$1- (1 - 1/m)^{nk}$
- 那么查询阶段,若对应某个待查询元素的k 的bit全部置位为1,则可判定其在集合中。因此某元素误判率p为:$(1- (1 - 1/m)^{nk})^k$
p = $(1- (1 - 1/m)^{nk})^k ~ (1 - e^{- nk/m})^k$
显然,当m越大,n减少时,误判率就越低。并且当k越大,误判率p也就越小,也就是说,hash函数越多,误判率越低,但相对检索的速度会越慢。
如图:相同位数组长度的情况下,随着哈希函数的个数的增长,误判率显著的下降。
布隆过滤器的效率和缺点
布隆过滤器的空间复杂度为 O(m) ,插入和查询时间复杂度都是 O(k) 。 存储空间和插入、查询时间都不会随元素增加而增大。 空间、时间效率都很高。
但是布隆过滤器并不支持删除元素,因为多个元素可能哈希到一个布隆过滤器的同一个位置,如果直接删除该位置的元素,则会影响其他元素的判断。因此,就提出了 计数布隆过滤器
计数布隆过滤器
计数过滤器(Counting Bloom Filter)是布隆过滤器的扩展,标准 Bloom Filter 位数组的每一位扩展为一个小的计数器(Counter),在插入元素时给对应的 k (k 为哈希函数个数)个 Counter 的值分别加 1,删除元素时给对应的 k 个 Counter 的值分别减 1。
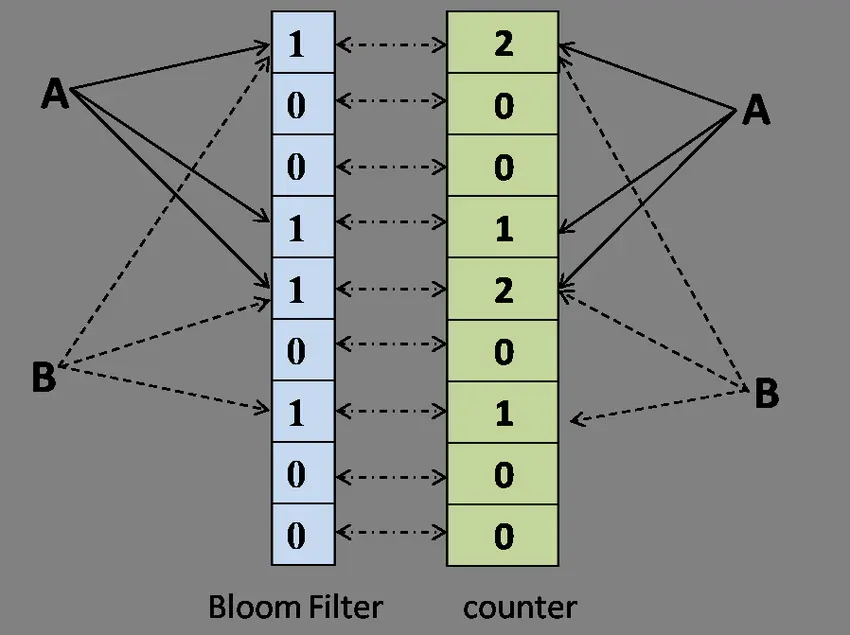
显然,又引入了另一个问题:更多的资源占用,而且在很多时候会造成极大的空间浪费
使用场景
Redis的缓存穿透
对于一个数据查询,其过程大致如下:
但是当查询的数据既不在缓存中,也不存在数据库中,则没有办法回写缓存,当有类似这样大量的请求访问服务时,数据库的压力就会极大。这就是缓存穿透
因此,引入布隆过滤器,当用户请求时,判断过滤器中是否存在该元素,若不存在该元素,则直接返回不存在。若包含则从缓存中查询数据,若缓存中也没有,则查询数据库并回写到缓存里,最后给前端返回。
尽管布隆过滤器有少量的误判,即可能不存在的数据会判定存在,从而继续查询缓存和数据库,但只要将m和k的值设置相对理想,少量的不存在查询也是可以接受的。
元素删除场景
实际上,元素不仅仅是只有增加,还存在删除元素的场景,比如说商品的删除,删除后数据其实已经不存在了,但是布隆过滤器中还没删除,则会判定其存在。
第一种方案就是使用计数布隆过滤器。
第二种方案,则是通过 定时重新构建布隆过滤器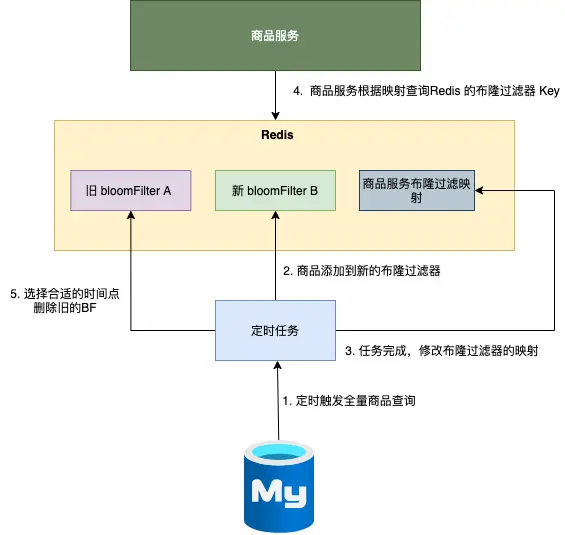
- 定时任务触发全量商品查询,更新数据;
- 将商品添加到新的布隆过滤器 ;
- 修改商品布隆过滤器的映射(从旧 A 修改成 新 B );
- 商品服务根据布隆过滤器的映射,选择新的布隆过滤器 B进行相关的查询操作 ;
- 选择合适的时间点,删除旧的布隆过滤器 A。
在删除商品 到 使用新的布隆过滤器B 之间的这段时间的不存在的查询有可能还会到数据库层面,但这种少量的不存在查询也是可以接受的。
应用布隆过滤器
Redisson
Redisson 提供了操作布隆过滤器的简单易用 API,以下是使用布隆过滤器的示例:
- 引入依赖
<dependency>
<groupId>org.redisson</groupId>
<artifactId>redisson</artifactId>
<version>3.37.0</version>
</dependency>- 使用示例
private void redisson() {
RedissonClient redissonClient = Redisson.create();
RBloomFilter < Object > bloomFilter = redissonClient.getBloomFilter("bloomFilter");
// 初始化大小为 10亿,假阳率为 0.001(在使用布隆过滤器之前,必须完成初始化操作)
bloomFilter.tryInit(1000000000, 0.001);
Object object = new Object();
// 添加元素
bloomFilter.add(object);
// 检查元素是否存在
boolean exist = bloomFilter.contains(object);
}Guava
Guava 也提供了 BloomFilter 实现,用于高效地判断一个元素是否存在于集合中,在 23.0 及之后版本中,是线程安全的。以下是 Guava 中布隆过滤器使用示例:
- 引入依赖
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<!-- 请根据需要选择合适的版本 -->
<version>33.3.1-jre</version>
</dependency>- 使用示例
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
public class BloomFilterExample {
public static void main(String[] args) {
// 创建一个布隆过滤器,预计插入 3000000 个整数,假阳率为0.01
BloomFilter < Integer > bloomFilter = BloomFilter.create(
Funnels.integerFunnel(), 3000000, 0.01);
// 向布隆过滤器中添加元素
for (int i = 0; i < 3000000; i++) {
bloomFilter.put(i);
}
// 测试布隆过滤器
for (int i = 0; i < 3001000; i++) {
if (bloomFilter.mightContain(i)) {
System.out.println(i + " might be in the filter.");
} else {
System.out.println(i + " is definitely not in the filter.");
}
}
}
}布隆过滤器总结
布隆过滤器的空间效率O(m) 和查询时间O(k) 都很优秀,但是存在一定的误判率 (布隆过滤器认为不存在,则一定不存在;布隆过滤器认为存在,则只是可能存在)
bit数组的位数m越大,hash函数的个数k越多,误判率就越低。但也需要控制合适的大小,比如m越大,但存储的数据少,则会引起空间浪费,k的个数越多,则会一定程度降低查存效率
普通布隆过滤器无法删除元素,但可以通过计数布隆过滤器和定时重新构建布隆过滤器两种方案实现删除元素的效果。
拓展:布谷鸟过滤器
布隆过滤器不记录元素本身,并且存在一个位被多个元素共用的情况,所以它不支持删除元素。布谷鸟过滤器(详细了解可以参考这篇论文《布谷鸟过滤器:实际上优于布隆过滤器》)的提出解决了这个问题,它支持删除操作,此外它还带来了其他优势:
- 查找性能更高:布隆过滤器要采用多种哈希函数进行多次哈希,而布谷鸟过滤器只需一次哈希
- 节省更多空间:布谷鸟过滤器记录元素更加紧凑,论文中提到,如果期望误报率在 3% 以下,半排序桶布谷鸟过滤器每个元素所占用的空间要比布隆过滤器中单个元素占用空间要小
布谷鸟过滤器之所以被称为“布谷鸟”,是因为它的工作原理类似于布谷鸟在自然界中的行为。布谷鸟以将自己的蛋产在其他鸟类的巢中而闻名,这样一来,寄主鸟就会抚养布谷鸟的幼鸟。
在布谷鸟过滤器中,如果一个位置已经被占用,新元素会“驱逐”现有元素,将其移到其他位置。这种“驱逐”行为类似于布谷鸟将其他鸟蛋推出巢外,以便安置自己的蛋。因此,这种过滤器得名为“布谷鸟”过滤器。
布谷鸟过滤器本质上是一个 桶数组,每个桶中保存若干数量的 指纹(指纹由元素的部分 Hash 值计算出来)。定义一个布谷鸟过滤器,每个桶记录 2 个指纹,5 号桶和 11 号桶分别记录保存 a, b 和 c, d 元素的指纹,如下所示:
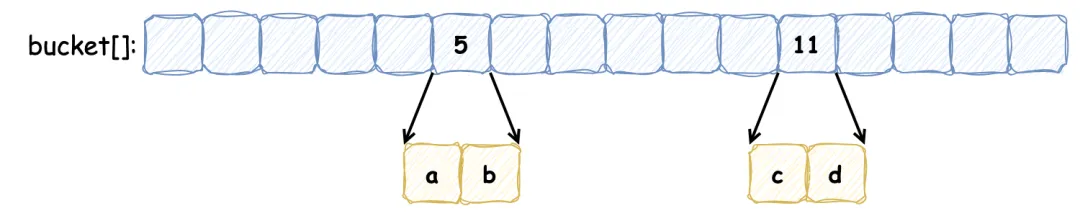
此时,向其中插入新的元素 e,发现它被哈希到的两个候选桶分别为 5 号 和 11 号,但是这两个桶中的元素已经添加满了:
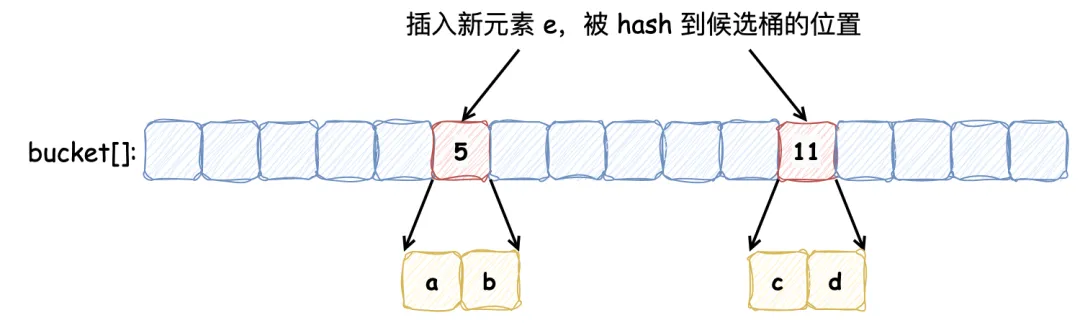
按照布谷鸟过滤器的特性,它会将其中的一个元素重哈希到其他的桶中(具体选择哪个元素,由具体的算法指定),新元素占据该元素的位置,如下:

以上便是向布谷鸟过滤器中添加元素并发生冲突时的操作流程,在我们的例子中,重新放置元素 e 触发了另一个重置,将现有的项 a 从桶 5 踢到桶 15。这个过程可能会重复,直到找到一个能容纳元素的桶,这就使得布谷鸟哈希表更加紧凑,因此可以更加节省空间。如果没有找到空桶则认为此哈希表太满,无法插入。虽然布谷鸟哈希可能执行一系列重置,但其均摊插入时间为 O(1)。
与布隆过滤器一样,布谷鸟过滤器同样会造成假阳性,造成假阳性的有以下原因:
- 有限的空间:布谷鸟过滤器使用有限数量的桶和每个桶中的有限空间来存储元素的指纹。当多个元素的指纹映射到相同的桶时,可能会导致不同元素的指纹存储在同一位置
- 指纹冲突:由于指纹是元素的哈希值的缩减版本,可能会有不同的元素产生相同的指纹。当查询一个不存在的元素时,可能会发现其指纹已经存在于过滤器中,从而导致假阳性
- 哈希函数的性质:哈希函数的选择和指纹长度决定了指纹的唯一性和冲突概率。较短的指纹更容易产生冲突,从而增加假阳性的概率
- 负载因子:随着过滤器接近满载,冲突的概率增加,这会导致更多的“驱逐”操作。在高负载情况下,假阳性率也可能上升
Github - cuckoofilter 是 Github 上 Star 数较多的一个仓库,它参考了论文内容,并用 Golang 实现了布谷鸟过滤器,大家感兴趣的话可以直接去参考它的源码。该过滤器重要的参数如下:
- 每个元素有 2 个候选桶,每个桶记录 4 个指纹:该配置能够使桶的利用率达到 95%,能够满足多数场景,当指定假阳性率在 0.00001 和 0.002 之间时,可以将每个元素占用空间最小化
- 指纹的静态大小为 8 位:指定误报率为 0.03,根据公式
f >= log2(2b/r)b为桶的大小 r为误报率,计算出指纹大小为 8。在 2 个候选桶和 4 个指纹的配置下,随着指纹大小变大,空间利用率不会再随之增加,仅降低假阳率
我们在此讨论下它的删除方法实现:
// Delete 删除过滤器中的指纹
func (cf *Filter) Delete(data []byte) bool {
// 尝试在首选桶中删除
i1, fp := getIndexAndFingerprint(data, cf.bucketPow)
if cf.delete(fp, i1) {
return true
}
// 删除失败,则尝试从备用桶删除
i2 := getAltIndex(fp, i1, cf.bucketPow)
return cf.delete(fp, i2)
}它的删除方法实现比较简单:它检查给定元素的两个候选桶,如果在首选桶中匹配到则将该指纹移除,否则去备用桶中匹配,在备用桶中则移除备用桶指纹,如果备用桶中没有,则会提示删除失败。如果两个元素 a, b 发生碰撞(共享桶和指纹),那么在 a 元素删除后,因为 b 元素的存在,仍然会判断 a 元素在过滤器中,表现出假阳性。需要注意的是,想要安全的删除某元素,必须事先插入它,否则删除插入项可能会无意中删除共享指纹的真实存在的项,而且如果多次插入重复元素,想要将其删除干净还需要知道该元素插入了多少次。
此外,相比于布隆过滤器它也存在一些的劣势:
- 插入性能可能会受到影响:随着插入元素越多,空间利用率不断提高,发生冲突的可能性越大,发生冲突之后,可能会不断的触发元素的重定位,插入性能会变差,一般通过最大重试次数来限制
- 插入重复元素次数存在上限:布隆过滤器插入重复元素没有负面影响,只是再标记相同的位,而布谷鸟过滤器插入重复元素会触发元素的重定位,因此它的重复元素插入存在上限
对于过滤器缓存的使用,大部分情景都是读多写少的,而重复插入并没有什么意义,布谷鸟过滤器的删除虽然不完美但总好过没有(因为布隆过滤器想要删除元素便需要重建,上亿甚至几十亿的数据重建缓存也蛮花时间),同时还有更优的查询和存储效率,应该说在绝大多数情况下其都是一个性价比更高的选择。